Lógica proposicional preuniversitaria [Guía completa]

 Álgebra preuniversitaria (Hydra´s notes) clase 1: Lógica Proposicional

Introducción:

Bienvenidos a la primera clase del blog de álgebra preuniversitaria, en esta entrada estaré abordando "todo" el tema de álgebra proposicional. Cabe aclarar que solo encontrarán lo necesario para el nivel preuniversitario respecto a este curso y lo necesario para comprenderlo, información extra se puede encontrar en el tema de lógica de filosofía (tengo planeado a futuro crear una entrada sobre esto en el blog de humanidades y actualizar esta publicación).

El contenido presente a continuación te puede ser de mucha ayuda si estas empezando a estudiar y tienes muy poco conocimiento del tema pues encontrarás explicaciones detalladas, formas de memorizar y una variedad de ejemplos, si ya eres un experto en este tema puede que lo veas como innecesariamente extenso, por ello, te invito a tomar el rol de "jurado" y calificar la forma de enseñar en esta entrada, puedes escribir tu reseña en los comentarios y así me estarías ayudando a mejorar el contenido para que sirva a más personas.

Información que puedes encontrar aquí:

1. Definiciones y desarrollo (Proposición lógica, conector lógico, proposiciones simples y compuestas, fórmula lógica, tabla de verdad, álgebra proposicional)

2. Formas de memorizar, observaciones para cada subtema y demostraciones para facilitar la comprensión.

3. Ejercicios sencillos para empezar a familiarizarse con el tema.

4. Enlace a la entrada con problemas resueltos, separados por tipos y niveles de dificultad tratando de simular el punto de vista de un principiante .

Información extra sobre el contenido de las entradas puede ser encontrado al abrir el enlace.

Recuerdo que cuando estaba en clases, muchos solían prestar poca atención a las definiciones y se limitaban a memorizarlas o pasaban de ellas para centrarse en los ejercicios pues al fin y al cabo "solo importa el poder resolverlos" para ingresar a una universidad. Esto último puede ser respaldado por muchos y rechazado por otros. Sin embargo, quiero tomar cierto enfoque con los blogs y por ello les recomiendo darle la misma importancia a las definiciones y ejercicios.

Con esto aclarado, antes de pasar a la información necesaria para resolver ejercicios, debemos preguntarnos lo siguiente.

¿Qué es una proposición lógica?

De forma simple, una proposición lógica es un enunciado sobre un sujeto definido que puede calificarse como verdadero o falso en cualquier circunstancia.

NOTAS: 

- Los dos posibles valores (V o F) que una proposición puede tomar son llamados "valores de verdad".

- Las proposiciones deben tener sentido completo por si solas (se explicará mejor en "tipos de proposiciones").

- Toda proposición puede ser "reemplazada" por una letra diferente para cada una, por lo general, minúscula a partir de la "p" en el alfabeto (p, q, r, s...). Ver paréntesis al lado de los ejemplos.

- Informalmente (y SOLO para este curso) podemos decir que una proposición es un enunciado y este otro es una oración. Asimismo, una proposición puede ser una expresión matemática (igualdad, desigualdad, ver ejemplos 7 y 9).

- Por sujeto definido entendemos a algo o alguien con un nombre (propio o común) que da a entender a que o a quien nos referimos (ver ejemplo 2)

- Para que un enunciado sea proposición se tiene que poder atribuirle un valor de verdad. (ver ejemplo 10)

Para que no quede duda alguna sobre esta definición y las notas, veamos algunos ejemplos.

EJEMPLOS DE PROPOSICIONES Y DE NO PROPOSICIONES

- Es proposición:

1. Alfonso es un hombre  (p)

3. El carro es azul             (q)

5. Pool será doctor            (r)

7. 4+4=8                           (s)

9. 1+1>0                           (t)

- No es proposición:

2. Él es un astronauta

4. Alfonsa es guapa

6. ¡Hace frío!

8. a+3=7

10. ¡Come tu almuerzo!

 Notas sobre los ejemplos:

1. Podemos decir que la proposición es verdadera o falsa con ver a la persona con nombre "Alfonso" (Se que muchas personas pueden llamarse igual pero podemos identificarlas que es lo que importa).

2. "Él" no es una persona identificable, no sabemos quien es "él" pues puede referirse a cualquiera (imagina que dos personas están solas y uno de ellos dice la oración "Él es X", sin señalar ni nada de indicaciones, la otra persona estará confundida pues no sabrá a quien se refiere).

3. Podemos decir que es V o F con solo ver el carro.

4. La belleza es algo subjetivo, varia de persona en persona por lo que no podemos dar una respuesta absoluta.

5. Podemos darle un valor a futuro, cuando podamos verificar si se cumplió o no.

6. En general el frío es algo subjetivo, diferentes personas pueden tener una distinta sensación térmica a una misma temperatura. (Se que en situaciones específicas como bajo cero podemos decir que la proposición es verdadera pero la idea de estos tipos de ejercicios es encontrar casos donde la respuesta pueda variar, este consejo se aplica para muchas preguntas de verdadero o falso). En todo caso, necesitamos un mayor contexto para dar una respuesta definitiva.

7. Por teoría de suma sabemos que es verdad.

8. "a" puede tomar cualquier valor, con "a=4" la proposición es verdadera pero con cualquier otro valor se vuelve falsa y eso va en contra de la definición al poder tener ambos valores.

9.1+1 nunca será menor o igual a 0 por lo que es verdad.

10. Esta expresión es una orden, no se le puede calificar como verdad o falsedad. De forma parecida, una pregunta como "¿Qué día es hoy?" no sería proposición por tener una respuesta diferente a V o F.

---

Puede que algunos se hayan preguntado algo respecto a los siguientes ejercicios 

- En la N°3, si no definimos un escenario, podría ser V o F.

- En el caso de la N°5, suponiendo que estamos en el presente, también podría ser V o F.

- Para la N°8, al ser "a" una variable que adopta cualquier valor por no estar definida, su ejemplo podría tener ambos valores de verdad.

Entonces, ¿Por qué los ejercicios 3 y 5 son proposiciones y el 8 no?

- Pasa que, al definir un escenario para los 3 ejemplos, el 3 y 5 tienen únicamente una posibilidad, para el primero el carro tendrá algo de color azul o simplemente estará ausente de este, para el segundo, o Pool llega a ser doctor o simplemente no lo será. Notamos que para ambos casos solo es posible que tengan un valor de verdad. En el caso de la variable "a", esta de por si puede adoptar cualquier valor, con uno de ellos será V o con los demás será F, no obstante, el valor que adopte depende enteramente de nosotros, no como los anteriores casos que escapan de nuestro control, 2 personas pueden elegir distintos valores para esta variable y por ello el ejemplo no tiene una respuesta definitiva.

- Imagina que estas con un amigo frente a una cortina que te impide ver que hay detrás y ponte en los escenarios 3, 5 y 8.

- Al abrirse esta cortina, podrás tener una respuesta única para los primeros 2 escenarios.

- Para el último caso, seguiríamos viendo la expresión matemática "a + 3 = 7". A fuerzas tienes que ser tú y tu acompañante quienes le den un valor según lo que cada uno quiera y estos pueden ser diferentes.

¿Ahora se entiende?

---

- Puede que muchas aclaraciones sean un tanto obvias pero quiero asegurarme de que todos sean capaces de entender, espero que no quede duda alguna, en todo caso, dame tu opinión de esto en los comentarios o en el servidor de discord.

 

Muy bien, ahora que conocemos lo anterior, es hora de aprender que son los conectores lógicos y como afectan a las proposiciones.

Definición de conectores lógicos

"Son palabras que tienen la capacidad de afectar a una proposición o conectarla con otra y cambiar su valor de verdad. A su vez, estos pueden ser representados con símbolos"

---

Nota:

Se llama OPERACIÓN LÓGICA a la capacidad de uno o mas conectores para afectar a una proposición o conectar varias y generar una nueva.

---

Ya que sabemos la definición, podemos identificar algunos tipos de conectores.

Estos se dividen en 6 clases con una gran variedad de ejemplos para cada una, a continuación veremos los más comunes en el siguiente cuadro:

Observación de la condicional:

Si bien es cierto que los conectores de consecuencia y causa ("porque", "ya que", "debido a que", etc) entran en la clase de "condicionales", estos son llamados "condicionales inversas o indirectas" porque invierten el orden de las proposiciones que unen. Para no confundirnos con esta clase de conectores deberemos de tener en claro que primero va la causa y luego la consecuencia.

Este ejemplo esta un poco adelantado pero quedará claro al ver las fórmulas lógicas un poco mas adelante.

Ejemplo: Mario terminó su carrera universitaria porque su madre le pagó la universidad.

p: Mario terminó su carrera universitaria

q: Su madre le pagó la universidad

Conector:  condicional - porque

Lo que pensaríamos sería en haces algo así: "p → q", sin embargo, al ser la palabra "porque" un conector condicional inverso la fórmula lógica quedaría de la siguiente manera: "q → p"

Esto es un poco sencillo de entender, solo tenemos que identificar que pasó primero, ¿La proposición "p" o "q"?

Es lógico decir que primero la madre de Mario le pagó su universidad para que él pueda terminar su carrera.

De otra forma, podríamos mover la proposición "p" al final de la oración y quedaría así: "Porque su madre le pagó la universidad, Mario terminó su carrera universitaria"

Recuerda esta observación cuando te topes con este tipo de conectores, no son muy comunes de ver en ejercicios de álgebra pero mas vale prevenir.

No te preocupes si no lograste entender del todo el ejemplo anterior, como dije, esta un poco adelantado, mas abajo esta la explicación del proceso de "simbolización/formalización" de las proposiciones y conectores, una vez lo veas puedes regresar aquí si te quedaron dudas.

Algunas notas y opciones para memorizar:

- Recomiendo memorizar y asociar las palabras mas representativas de cada grupo de conectores con su clase, su símbolo y el contexto en que se usan. Para esto el cuadro te será de mucha ayuda.

 + Por ejemplo: 

Al ver el nombre de la clase "negación", casi inconscientemente se nos viene a la mente el "no" pues su propio nombre hace referencia a este, ahora solo tenemos que incluir el "~" a la asociación y así lo podremos recordar cada vez que lo necesitemos. Asimismo, al tener en mente que se trata de palabras de "negación", podemos crear ejemplos propios como el "ni" o el "nunca" sin necesidad de memorizarlos.

En pocas palabras:

Conector: Negación

Palabra representativa: "No"

Asociación: Negación = No = ~ = Palabras que impliquen negar algo.

 + Mas ejemplos de asociaciones:

- En el caso de la conjunción, podemos asociar el "Ʌ" con la letra representativa "y", imagina que la "y" va abajo del "Ʌ", puedes visualizar que encajan muy bien, solo tienes que recordar esto y tener mucho cuidado de no confundirlo con el símbolo de la disyunción. Esto se puede aplicar cuando vayamos a memorizar la tabla de la conjunción.

- En el caso de la disyunción débil, podemos notar que la "V" se asemeja a una "u" y al recordar la "u" se nos vendrá a la mente la "o" y que el contexto es de elecciones (que solo puedes elegir una opción entre 2). 

- Otra forma de lograr lo anterior seria asociar la palabra "disyunción" con "disyuntiva", la cual se usa en situaciones de elección que son excluyentes (Lo uno o lo otro) y así recordar los conectores "o" y "u".

- En el caso de la bicondicional puedes decir que el "Bi" hace referencia a que hay el doble de algo, su símbolo es el "↔" que coincidentemente tiene flechas a ambos lados, solo asocia el "bi" con las 2 flechas y serás capaz de recordarlo, también puedes asociar esto con el contexto que te indica el nombre "bicondicional", significa que los conectores deben de ser de "condición absoluta" como el "si y solo si" (seria algo como resaltar un requisito)

 - Un ejemplo de lo anterior es: "Iré al gimnasio si y solamente si me compras un helado", podemos notar que el conector le esta dando mucha importancia a la condición a diferencia de la clase condicional que son un poco mas generales.

---

ACLARACIÓN:

Estas asociaciones son algo difíciles de explicar en palabras y las he tenido que resumir demasiado para no salir mucho del tema. En todo caso solo son una alternativa entre las infinitas maneras de recordar algo cuyo límite es la imaginación, si ya has memorizado la teoría y puedes decirla a la velocidad de un "chasqueo" cuando así lo quieras probablemente no te sirva de mucho aprenderlo de esta forma.

Puedes decidir seguir estos ejemplos al pie de la letra pero recomiendo que te quedes con la "esencia" y la adaptes a tus necesidades, cada uno es diferente y la mejor asociación será aquella con la que te sientas mas cómodo/a.

En mi opinión, esto sirve en casos donde vas a empezar a memorizar algo y a la larga es mucho mas efectivo que ir repitiendo o escribiendo en una hoja hasta que nuestro cerebro se lo grabe, siempre que encuentres una asociación adecuada claro está.

El chiste de todo esto es crear bloques de información, si memorizas cada concepto de forma aislada existe el riesgo de olvidarlo al no usarlo por mucho tiempo, sin embargo, cuando tienes información entrelazada (asociada) existe una menor probabilidad de que la olvides pues un dato te haría recordar otro.

Tengo una guía sobre el estudio autodidacta donde hablo de estas técnicas mas a fondo, reflexiones y mucho más, puedes verla haciéndole click.

Si conoces otras formas de memorizar, puedes compartirlas en los comentarios.

Si quieres aprender aún mas sobre estos métodos, puedes preguntármelo en el grupo de discord de los blogs, por lo general estoy disponible.

---

Antes de continuar haremos un pequeño paréntesis pues ahora que conocemos el significado de "conector lógico", podemos definir y entender 2 tipos de proposiciones.

Proposiciones simples y compuestas

- Una proposición recibe el nombre de proposición simple cuando no presenta conectores lógicos que la afectan.

- Una proposición compuesta es aquella que:

 1. Presenta una proposición afectada por un conector lógico.

2. Contiene 2 o mas proposiciones enlazadas mediante conectores lógicos.

Nota:

- Hay que tener muy presente las definiciones de "proposición" y "conector lógico" para no cometer errores (ver la resolución del primer ejercicio)

Para ir familiarizándonos con los nuevos términos, te propongo que resuelvas los siguientes ejercicios calificándolos como "Proposición simple (PS)", "Proposición compuesta (PC)" o "No es proposición (NP)", podrás ver las respuestas mas abajo.

Tomate el tiempo que consideres necesario, aquí no hay prisas.

Ejercicios de identificación de proposiciones simples y compuestas

1. Enrique y Joseph son amigos.

2. No es verdad que Yair sea astronauta.

3. Nicol es buena amiga.

4. ¿Qué día es hoy?

5. Tu hermano irá al cine contigo si y solo si termina sus tareas a tiempo.

6. El gato es un mamífero.

SOLUCIONES:

1. (PS) 

- Puse primero este ejercicio para aclarar lo siguiente, es una proposición simple porque el conector "y" no esta cumpliendo su función como conector lógico pues no añade proposiciones. En este caso el "y" solo esta listando a los sujetos "Enrique" y "Joseph". Además, "Enrique" por si solo no es una proposición, es un sustantivo, tenemos que tomar en conjunto a los dos para que la proposición tenga sentido.

OBSERVACIÓN:

- Lo anteriormente dicho también se cumple porque se dice que los sujetos son "amigos", no es posible decir que "Enrique es amigo" o que "Joseph es amigo" ya que no tienen sentido completo y por ello no se pueden encontrar 2 proposiciones. Si el caso fuera "Enrique y Joseph son paramédicos", la proposición sería compuesta pues existiría la proposición "Enrique es paramédico" y "Joseph es paramédico", notemos que cada proposición por separado tiene sentido completo. El tipo de proposición en casos como este dependerá del predicado.

2. (PC)

Para resolver este ejercicio tenemos que identificar la proposición y el conector lógico

- Primero, para entender mejor, podemos decir que "Yair sea astronauta" es igual a "Yair es astronauta"

- Observamos que el arreglo facilita la comprensión y que cumple con las características de una proposición pues puede ser calificada como verdadero o falso y el sujeto esta definido.

- En segundo lugar, identificamos el conector lógico, para ello nos tenemos que preguntar a que nos recuerda "No es verdad", muy probablemente recuerdes que al ser estar negando algo viene a ser un ejemplo de conector de negación.

- Con lo anterior encontrado, podemos decir que cumple los requisitos del caso 1 para ser una proposición compuesta.

3. (NP)

- Si recuerdas las observaciones de los ejemplos de proposiciones lógicas, fácilmente dirás que este caso no es el de una de ellas pues su valor de verdad puede variar y eso va en contra de la definición.

4. (NP)

- No es proposición porque es una pregunta y no se puede asignarle un valor de verdad. Una vez mas, podíamos llegar fácilmente a la respuesta al recordar los primeros casos.

5. (PC)

- Esto lo resolveremos por partes como el ejercicio 2

- En primer lugar, identificaremos las posibles proposiciones.

- Vemos que "Tu hermano irá al cine contigo" es una proposición.

- Ahora viene algo que puede ser confuso si se ve por primera vez o si se sobrepiensa.

- "... termina sus tareas a tiempo" ¿Es o no es una proposición? Puede que algunos digan que no lo es porque no tiene un sujeto definido, sin embargo, debemos tomar la oración completa para ver que, efectivamente, si es una proposición pues el sujeto se había dicho al comienzo. Podríamos decir que estaba incompleta si la veíamos aisladamente.

- De esta forma, "Tu hermano irá al cine" y "Tu hermano termina sus tareas a tiempo" son dos proposiciones, digamos que serán "p" y "q"

- Luego de esto, identificaremos el conector lógico el cual es "si y solo si", este viene a ser un caso de bicondicional.

- Al identificar todo lo anterior, podemos afirmar que es una proposición compuesta.

6. (PS)

- No hay mucho que decir, es un ejemplo muy básico de proposición simple.

Con esto aclarado, es hora de continuar.

Es importante recordar que cada proposición puede "resumirse" con el uso de una letra minúscula, al realizar este cambio la letra que simboliza a la proposición recibe el nombre de FÓRMULA LÓGICA.

De esta forma, la proposición "Fernando es doctor" pasaría a ser la letra "p".

Sin embargo, este nuevo concepto puede abarcar mas de una proposición a la vez.

¿Qué es una fórmula lógica? y algunos ejemplos

"Es la representación simbólica de una o más proposiciones y de su interacción con los conectores lógicos"

Ahora que sabemos que son los conectores lógicos, sus respectivos símbolos y la cualidad que tienen las proposiciones de poder representarse a través de letras, somos capaces de entender el concepto de fórmula lógica. No saber alguno de los anteriores puntos nos habría impedido comprender del todo esta nueva definición.

A continuación, te propongo algunos ejercicios para recordar y practicar lo anteriormente visto.

Para resolverlos tendrás que:

Identificar las proposiciones, conectores lógicos y elaborar su fórmula lógica.

Una vez mas, usa tanto tiempo como requieras, no te apures y revisa antes de dar una respuesta definitiva.

1. Noelia y Ramón son amigos ya que se ayudan mutuamente.

2. Hernando es doctor y Cielo es astronauta.

3. Mi hermano Enrique no come sus verduras.

4. O estudio para mi práctica o juego videojuegos con mis amigos.

5. Si Joseph aprueba su examen de Álgebra y Raúl su práctica de fútbol entonces iremos al parque.

RESOLUCIONES:

No seré tan específico en el desarrollo de ejercicios parecidos a los anteriores ni en explicaciones ya hechas para no redundar.

1. 

¿Recuerdan la observación sobre las condicionales inversas? Aquí se va a aplicar ello

- Noelia y Ramón son amigos (p)

- (Noelia y Ramón) se ayudan mutuamente (q)

- Conector: Condicional inverso -  ya que

- Fórmula lógica: q → p

La explicación es la misma que la de la observación hecha anteriormente, pueden verla debajo de la imagen de los conectores lógicos. Si siguen teniendo dudas háganlas en los comentarios.

2.

- Hernando es doctor (p)

- Cielo es astronauta (q)

- Conector: Conjunción - "y"

- Fórmula proposicional: "p Ʌ q"

- El primer "y" de Hernando y Cielo no es conector y ha sido explicado anteriormente.

3.  

- Mi hermano Enrique come sus verduras (p) 

- Conector: Negación - "no"

- Fórmula proposicional: "~p" 

- "p" es la afirmación de toda la proposición compuesta "~p" o dicho de otra forma, la proposición simple. Debemos recordar que las proposiciones que simbolicemos deben ser simples pues conectores como los de negación también deben ser simbolizados.

4. 

- Estudio para mi práctica (p)

- Juego videojuegos con mis amigos (q)

- Conector: Disyunción fuerte - O...o

- Fórmula lógica: "p △ q"

- Cabe mencionar que las dos "O" simbolizan a un solo conector, no dos.

5. 

Este ejercicio lo dejé para el final ya que merece ser comentado.

- Joseph aprueba su examen de Álgebra (p)

- Raúl (aprueba) su práctica de fútbol (q)

- (Nosotros) Iremos al parque (r)

---

Aclaración:

El pronombre "nosotros" esta definido porque todos los sujetos a quienes hace referencia son conocidos (Joseph, Raúl y yo). El "yo" literalmente es el lector en ese escenario y uno se conoce a si mismo.

---

Podemos notar que es la primera vez que tenemos a una tercera proposición en un ejercicio. No obstante, no debemos sentir temor alguno pues la resolución es la misma. Es mas, por lo general es muy común ver ejercicios con un mínimo de 3 proposiciones.

- Conectores identificados: Condicional "Si...entonces" - Conjunción "y"

Siempre que resolvamos ejercicios de simbolización identificaremos las proposiciones y conectores de izquierda a derecha, cuando tengamos muchos de ambos haremos lo siguiente.

Escribir las proposiciones por orden de aparición                              :     "p       q        r"

¿Existe un conector condicional inverso?                                           :  Observamos que no

Ubicamos los conectores de tal forma que tengan sentido con la oración     :   p  Ʌ  q   →  r

Hemos puesto primero el conector "Ʌ" entre "p" y "q" porque ese completa su sentido en la oración primero. Para que el conector "→" tenga sentido, tenemos que leer toda la oración y por ello notamos que ocurre lo siguiente "Si p y q entonces r", por lo que va en segundo lugar. 

Para entender mejor esto del sentido le agregamos paréntesis a la fórmula :  (p Ʌ q) → r

Ahora sabemos que lo que esta dentro del paréntesis tiene prioridad pues tiene un sentido completo por si solo, luego obtendremos su resultado y procederemos con lo que queda. A continuación será resumido en una imagen.

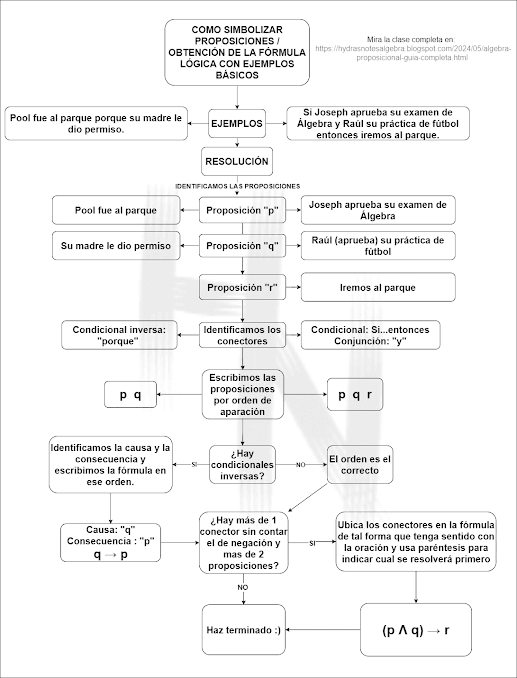
¿Cómo obtener una fórmula lógica? o como simbolizar proposiciones - Imagen descriptiva del proceso usando ejemplos básicos

Por cuestiones de espacio, recomiendo hacer click derecho a la imagen y abrirla en una pestaña nueva para verla en mejor calidad y con zoom

Llegados a este punto ya sabemos los conceptos básicos y pasos para conseguir la fórmula lógica de cuantas proposiciones queramos, lo único que nos faltaría es practicar mas. No obstante, todo lo anteriormente visto era la introducción a lo que nos compete para resolver ejercicios de álgebra en este tema. Conocemos como obtener la fórmula lógica pero, ¿Cómo obtener el valor final de esta?

Para esto nos sirven las "tablas de verdad"

Tablas de verdad - Definición - Tipos - Consejos para memorizar y ejercicios básicos

¿Qué son las tablas de verdad?

"Una tabla de verdad es una herramienta que nos permite conocer el valor final de una fórmula lógica al detallar el estado de verdad de cada proposición y la naturaleza de sus interacciones con otras mediante conectores lógicos"

Podemos notar que hay un nuevo concepto en esta definición, aún no sabemos el significado de los "estados de verdad" de una proposición. Sin embargo, no es nada de otro mundo

¿Qué son los estados de verdad en lógica proposicional?

De forma simple, son los posibles valores que una proposición puede adoptar, V o F. Visto de forma conjunta, son las permutaciones (Informalmente, todas las combinaciones posibles) de los valores de las proposiciones.

Como ayuda, la cantidad de valores que toman varia según la cantidad de proposiciones presentes, tal como dice la siguiente regla.

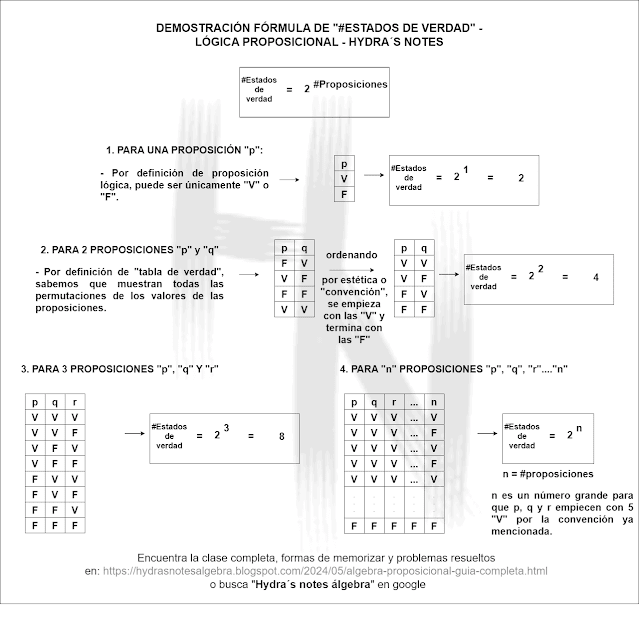
DEMOSTRACIÓN DE LA FÓRMULA "CANTIDAD DE ESTADOS DE VERDAD"

La cantidad de estados de verdad presentes en una tabla de verdad NO es dada por una fórmula sino que esta es el resultado de realizar varios ejemplos con diferentes proposiciones y encontrar un patrón que ha sido representado matemáticamente para servir de guía.

A continuación, podrás ver la demostración y entender de donde proviene la fórmula por si no lo sabías.

(En celular recomiendo hacer zoom a la imagen)

Como aclaración, diremos que cada proposición equivale a un número, siendo "p = 1" y "n= número total de proposiciones", siendo el último el que dicta la cantidad de veces que el "2" se multiplica a si mismo.

En cuanto a las permutaciones de valores (V o F), tiene un tema propio que cubriré en un futuro pero lo básico es fácil de entender, solo tienes que encontrar todas las formas posibles de ordenar los valores (en parejas en este caso) teniendo en cuenta que la posición importa (o sea que "VF" es diferente de "FV"). El hecho de que todas las proposiciones tengan los mismos posibles valores facilita mucho este último punto.

Con eso aclarado, creo que la demostración se entiende bastante bien por si sola así que continuemos.

Explicaciones mas detalladas sobre los valores de verdad: 

Hasta donde se, no existe una forma obligatoria de agrupar los valores de verdad de las proposiciones, no obstante, te RECOMIENDO que las agrupes como lo ves en la imagen de arriba (y en la demostración) para facilitar la comprensión y tener un orden, trataré de ponerlo en palabras aquí abajo.

- Escribe las proposiciones de izquierda a derecha (en orden alfabético). Ej: "p - q - r - s -..."

- Siempre empieza por "V" en cada valor de cada proposición y termina con "F" (esto nos servirá para ganar tiempo en algunas tablas de conectores lógicos).

- Para una proposición, primero pon una V y abajo una F. (ver ejemplo de "p" en la img.)

- Para dos, sabemos que tienen que tener 4 valores cada una, para la que va primero (p) separa sus valores de 2 en 2, dos V y dos F. Para la segunda (q), ve intercalando entre V y F hasta completar. (como en la imagen de ejemplo)

-  Para 3, agrupa los valores de "p" de 4 en 4; de "q" de 2 en 2 y de "r" intercalado como se explica arriba.

- EN GENERAL, los valores de la última proposición ordenada de forma alfabética (la que esta mas a la derecha) van intercalados, empezando siempre por "v"; los de la penúltima proposición van de 2 en 2, empezando por dos "v", para la antepenúltima los agrupas de 4 en 4 como ya sabes y así sucesivamente hasta llegar a la primera proposición en el orden anteriormente dicho (Puedes observar esto en la imagen donde se demuestra la fórmula de los estados de verdad).

Eso es todo lo que debemos de saber sobre los valores de verdad, ahora veremos las tablas de verdad para cada una de los conectores lógicos, verás una imagen de ejemplo con 2 proposiciones aquí abajo.

TABLAS DE VERDAD DE LOS CONECTORES LÓGICOS

Como en el subtema anterior, podemos observar lo siguiente.

- En el caso de la NEGACIÓN, solo afecta a una proposición a la vez (y todos sus posibles valores), a diferencia de los otros conectores, este no sirve para "unir" proposiciones. Su FUNCIÓN es invertir el valor de la proposición que afecte, si es "V" pasa a ser "F" y viceversa.

- Para las tablas de verdad de los otros conectores solo basta con que nos fijemos en las filas y reemplacemos los valores de "p" y "q" en cada conector.

Algunas formas de memorizar las tablas de verdad de los conectores lógicos:

1. Tal como esta escrito en forma de consejo en la imagen, es recomendable solo memorizar los casos en los que el valor de una tabla de verdad sea diferente a los demás de la misma tabla, los dos últimos conectores son algo mas flexibles en cuanto a esto.

Como ejemplo de lo anterior, veamos el caso de la conjunción, observamos que para que el resultado final sea "verdadero", los valores de "p" y "q" tienen que ser "V", este es el único caso de esta tabla que cumple con esto por lo que si lo memorizamos, sabremos que para cualquier otra combinación de valores de verdad, la respuesta será "F".

2. Otro ejemplo para el caso de la conjunción, ¿Recuerdas lo que mencioné anteriormente sobre el conector "y" y el símbolo "Ʌ"? Al poner la "y" debajo del "Ʌ" notamos que encajaban y así creábamos una asociación para memorizar el conector con su símbolo, si seguiste ese camino, ahora puedes reemplazar la "y" por la "V" y al hacer esto debes recordar que para que la conjunción sea verdadera, ambos valores de las proposiciones deben ser verdaderos. Si no consideras necesario lo anterior, podemos recordarlo al decir lo siguiente "V y V da V, caso contrario da F".

3. El símbolo de la disyunción es una "V" que nos hace recordar a la "u" y "o" y justamente el único caso donde su valor final es "F" es cuando ambas proposiciones son falsas. Una opción para recordar esto sería tomar un caso de opuestos, cada ves que veas el símbolo de una disyunción (V) asócialo con su opuesto (F) y que las proposiciones deben ser de ese mismo valor (F). Otra forma sería recordar esta frase "F o F da F, caso contrario da V".

4. Memorizar la tabla de la condicional es muy fácil, solo visualiza o memoriza "V → F = F", puedes repetirlo unas cuantas veces si te sientes mas cómodo, "V entonces F igual F". Todo caso diferente nos da "V"

5. Para el caso de la bicondicional les preguntaré si recuerdan mi forma de memorizarla, el hecho que "bi" hace referencia a  a que necesitamos "dos" iguales y que los extremos de su símbolo "↔" nos recuerda a la "V", solo fíjate en un extremo y justamente para que sus valores finales sean "V", los valores de las proposiciones tienen que ser iguales, dos "F" o dos "V".

En palabras simples el proceso sería así:

a. Vemos el símbolo de la bicondicional (↔)

b. Recordamos que los extremos de su símbolo implican que debe existir el doble de algo para que su valor sea verdadero (porque sus extremos parecen "V" ).

c. Ahora sabemos que si las proposiciones son dos V o dos F, entonces su valor final será "V", cualquier caso donde los valores sean opuestos nos dará "F".

Si aún te quedan dudas con lo anterior, recordemos que siempre empezamos por V y terminamos con F al colocar los valores de verdad, entonces la tabla de la bicondicional será V al principio y al final. Podemos usar esto para recordar casi todas las tablas de hecho.

6. La tabla de verdad de la disyunción fuerte es exactamente opuesta a la tabla de la bicondicional, si hacemos uso de la asociación anterior seremos capaces de recordar dos tablas a la vez.

Ejemplo: Si la bicondicional necesita dos valores iguales para ser verdadera, entonces la disyunción fuerte necesita dos valores idénticos para ser falsa. (ver imagen de arriba)

Y listo. He tratado de explicar de forma detallada mi manera de recordar estas tablas sin tener que memorizar todos los casos, espero que sea de ayuda para alguno de ustedes.

Conocemos las tablas de verdad, sin embargo, existen casos donde los valores finales pueden ser solamente verdaderos, falsos o una combinación de ambos, estas posibilidades reciben nombres específicos que debemos recordar.

1. TAUTOLOGÍA

- Cuando los valores finales de una tabla de verdad son únicamente "V", el resultado recibe el nombre de tautología.

2. CONTRADICCIÓN

- Se le llama contradicción al caso en el cual los valores finales son todos falsos.

3. CONTINGENCIA

- Cuando los valores de una tabla de verdad son una combinación de V y F, sin importar su proporción, se le llama contingencia.

Notas sobre su memorización:

Creo que es algo instintivo el asociar la palabra "contradicción" con lo "negativo" y por ende con la "F".

Otra opción es memorizarlas en este orden: "Tautología, contradicción y contingencia" y decir que a la primera le corresponde la "V", a la segunda la "F" y a la tercera una combinación de las anteriores.

De cualquier forma al ser definiciones simples solo basta con resolver unos cuantos ejercicios para que se graben en nuestra memoria.

Luego de ver todo lo anterior, es hora de ponerlo en práctica con algunos ejercicios básicos ya que de nada sirve aprender la teoría si no la aplicamos. Toma todo el tiempo que necesites y recuerda que encontrarás la resolución mas abajo.

Objetivo: Hallar el valor final de cada tabla de verdad y calificarlas como "Tautología, Contradicción o Contingencia".

1. (p V q) Ʌ (q V p)

2. (p → q) ↔ (q △ p)

3. (~q V ~p) V (p V q)

4. ~ (q Ʌ p) → (~ (p V q))

5. p V q V r

Resoluciones:

Para los primeros cuatro ejercicios, debemos recordar que los paréntesis nos indican la prioridad, primero se resuelve lo que este dentro. 

Luego de las explicaciones pueden encontrar 2 imágenes con la resolución de los ejercicios

Color celeste: Resultado final

Color amarillo: Proposiciones de la fórmula lógica que da el resultado final

1. Obtenemos los valores de lo que esta en paréntesis, los resultados obtenidos pasan a ser nuestras nuevas "proposiciones" estas están unidas por una disyunción que tendremos que resolver, al hacerlo, obtenemos una "contradicción".

2. Como en el caso anterior, resolvemos los paréntesis y los resultados los evaluamos mediante la tabla de la bicondicional, la podemos recordar con la frase aconsejada "V entonces F da F". Al final se llega a una contradicción

3. En el primer paréntesis (el de la izquierda), tenemos que resolver primero la tabla de la negación para "p" y "q", luego evaluamos los resultados con la tabla de la disyunción y así continuamos para obtener una tautología.

4. Al obtener el resultado del paréntesis de la izquierda, tenemos que cambiar su valor según lo indica la negación que observamos, realizamos un proceso similar en el paréntesis de la derecha y los resultados los evaluamos en la tabla de la condicional. Obtenemos una contradicción.

5. Este último ejercicio es algo peculiar pues observamos que todas las proposiciones tienen igual valor, ninguna es mas importante que otra, en casos como este, podemos empezar por donde queramos así como colocar paréntesis por donde empecemos si lo creemos necesario. En la imagen de abajo tenemos los 2 posibles caminos que nos llevan a una misma solución, ya sea empecemos por "p V q" o "q V r", los valores finales serán los mismos (Contingencia en este caso).

Observación:

Esta es una regla que funciona solo para la disyunción débil y la conjunción cuando veamos casos como este, los invito a verificarlo. Esta es una propiedad que veremos mas adelante.

Creo que muchos de ustedes encontrarán "innecesariamente largas" las resoluciones de problemas de lógica proposicional, los entiendo y yo también lo creo así. Sin embargo, la mayoría de ejercicios suelen ser aún mas largos, involucrando por lo general 3 o 4 proposiciones. Imagina lo que tardarías en resolverlos, para esos casos, se hace uso de unas "propiedades" que reciben el nombre de "Álgebra proposicional" y veremos a continuación.

Álgebra proposicional 

Por lo general, las "propiedades" que veremos a continuación son simples equivalencias lógicas de ciertas tablas de verdad. Antes de continuar, explicaré mejor este nuevo término.

---

¿Qué son las equivalencias lógicas?

Cada tabla de verdad de cada fórmula lógica tiene un resultado, cuando los valores finales de 2 o más fórmulas lógicas son iguales, se les llama "equivalencia lógica".

Mas que "iguales", la palabra correcta es "equivalentes" pues las fórmulas de donde provienen son diferentes pero informalmente se entiende mejor con el primer término, ¿no? Si no tienes confusiones respecto a las palabras, recomiendo aprender la definición usando la segunda.

Tomemos de ejemplo al ejercicio 1 de las tablas de verdad, el resultado final era "V V V F" que coincide con la tabla de la disyunción, la cual tiene los mismos valores finales. Entonces, podemos decir que la fórmula lógica del ejercicio 1 es equivalente a la tabla de la disyunción débil.

Ahora se entiende mucho mejor, ¿verdad?

Con esto aclarado sigamos comentando acerca del álgebra proposicional

---

Si la mayoría de las propiedades del álgebra proposicional son equivalencias, ¿significa que son prácticamente infinitas?

La respuesta es que sí, uno puede encontrar tantas equivalencias como quiera y perfectamente agregarlas a la lista del álgebra proposicional, no obstante, existe una lista que enumera las mas usadas y que justamente son las que nos servirán en la mayoría de problemas.

Antes de verlas, responderemos una última pregunta para resumir lo anteriormente dicho.

¿Para qué sirve el álgebra proposicional?

El uso del álgebra proposicional no es otro que proporcionar las equivalencias de ciertas fórmulas lógicas que podamos encontrar en un ejercicio así como su resultado inmediato en algunos casos. Memorizar estas abreviaciones nos permitirá ganar tiempo al resolver problemas pues no tendremos que elaborar una tabla de verdad para cada paso que demos.

Con esto entendido, es hora de conocer estos atajos.

Lista de propiedades mas usadas del álgebra proposicional y sus demostraciones

Recomiendo abrir las imágenes en una nueva pestaña para verlas en mejor calidad.

Algunas observaciones sobre las propiedades de la conjunción y disyunción débil:

- En ambos casos, la propiedad 3 es igual al ejercicio resuelto anteriormente con su demostración, pueden ver que era un pequeño adelanto a esto.

- La propiedad 4 para ambos casos es una distribución de "lo que esta fuera del paréntesis", se distribuye entre las proposiciones que están dentro y los nuevos resultados quedan unidos por el conector dentro del paréntesis.

---

Notas sobre las leyes de Morgan, absorción, condicional y falsa absorción y consejos para memorizarlas:

1. Tener en cuenta lo siguiente nos ayudará a entender, memorizar y aprender estas leyes, en especial las de Morgan.

- Al igual que el opuesto de V es F y viceversa, el opuesto de "V" es "Ʌ" y de una proposición "p" es "~p".

- El signo de la negación (~) nos indica que el valor afectado se vuelve su opuesto.

- Si el ~ se encuentra al lado izquierdo de un paréntesis, afecta a todo su contenido.

- Si tenemos "~(p V q)", el resultado será "~p Ʌ ~q" pues la negación afectó a todo el contenido del paréntesis (proposiciones y conector lógico).

Esto nos permitirá usar de forma intuitiva las leyes de Morgan sin tener que memorizarlas.

2. Notas sobre las leyes de la absorción para entenderlas mejor:

Para aplicar las leyes de la absorción, tenemos que ser capaces de identificar el siguiente patrón

"Proposición 1 + conector 1 + (Proposición 1/2 + conector 2 + proposición 2/1)"

o

"(proposición 1/2 + conector 2 + proposición 2/1) + proposición 1 + conector 1"

Donde proposición 1 y 2 son diferentes y los conectores 1 y 2 son de conjunción o disyunción.

Siempre y cuando reconozcamos lo anterior, podremos saber que el resultado es la proposición que esta afuera. Puede ser un poco complicado de entender por lo que una explicación mas simple esta aquí abajo.

Observación muy importante:

El primer patrón se encuentra en la imagen, en los casos 3 y 4 ["p V/Ʌ (p Ʌ/V q)"], sin embargo, si resolvemos el paréntesis no importará en que lado se encuentre lo que esta afuera, el resultado será el mismo. Esto hace posible el segundo patrón "(p Ʌ/V q) V/Ʌ p". 

También debes recordar la segunda propiedad de la conjunción y disyunción débil que dice que puedes intercambiar la posición de 2 proposiciones afectadas por alguno de esos dos conectores lógicos.

Ejemplo: p V (p Ʌ q) = p V (q Ʌ p)

Notamos que no importa el orden de lo que este dentro del paréntesis pues el resultado será el mismo. 

Por último, ¿Qué pasaría si negamos las "p"?, ¿El resultado sería el mismo o su negación?

Te invito a comprobar todo esto, elabora una tabla de verdad y empieza a tratar de demostrar las "propiedades". Ello te permitirá despejar tus dudas y reconocer variaciones de los casos del álgebra proposicional, en un problema no siempre se te dará el escenario idóneo para aplicar algún atajo, por lo general tienes que reconocer una variación de las propiedades. Al fin y al cabo, tu objetivo debe ser entender su "esencia" y no simplemente memorizarlas pues casos ligeramente diferentes van a aparecer y si no eres capaz de identificarlos demorarás mucho mas en resolver un problema o en todo caso no podrás hacerlo y creerás que la matemática no es para ti.

3. Notas sobre la falsa absorción para lograr entenderla: 

Algunas de las variaciones de la absorción se aplican a la falsa absorción, notamos que, al resolver el paréntesis, el resultado siempre será el mismo sin importar de que lado este la proposición y conector restante (recomiendo mirar las "demostraciones" y cambiar de lado mentalmente el "p V / p Ʌ" o hacerlo a mano en un papel). 

Con esto aclarado, entender el resultado de las leyes de la falsa absorción debe ser algo "intuitivo", si somos observadores, podemos ver que la primera parte de los resultados de estas leyes es igual a lo que esta fuera del paréntesis, a continuación lo sombreo en negrita "p Ʌ (~p V q) = p Ʌ q". Además de esto, la proposición restante es la que es diferente a la de afuera, en este caso sería "q". Creo que se entiende, si somos capaces de reconocer esto no tendremos que repetir una y otra vez hasta memorizarla.

Nota importante : Cabe resaltar que, en el caso 6, "(~p V q)" puede ser reemplazado por "(p →q)", pues es la propiedad 7 (caso de la condicional)", esta última puede ser recordada fácilmente con un truco que encontrarás a continuación.

4. Como memorizar fácilmente las propiedades de la condicional:

- A lo largo de esta entrada, he mencionado la similitud de la punta de la condicional y bicondicional con el símbolo "V", usaremos esta asociación para recordar la propiedad 7.

No se ustedes pero para mi el símbolo " → " es la unión de "~" y "V" rotada 90° a la izquierda. Usaremos esto para acordarnos de la propiedad.

Cada vez que veas "p → q", cambia la condicional por los símbolos ya mencionados, el "~" ponlo al lado izquierdo y queda así "~p", y la "V" déjala donde antes estaba el "→", quedaría lo siguiente: "~p V q". A continuación les dejo un video que representa lo anterior, es la primera vez que hago esto por lo que espero que sea por lo menos "decente".

Puedes ver las viñetas de canvas aquí

- Para la otra propiedad de la condicional, solo bastará con recordar esto: "Proposiciones negadas, proposiciones cambiadas".

Tenemos esta fórmula lógica "p → q", lo que vamos a hacer es lo siguiente, cambiamos las proposiciones por su negación ("p" por "~p" y "q" por "~q") y las intercambiamos.

Quedaría así: "~q → ~p"

Ahora deberías ser capaz de recordar esta propiedad de forma fácil y sencilla.

---

Algunas notas sobre el álgebra proposicional de la bicondicional y disyunción excluyente:

- Las propiedades 1 y 6 son conocidas como "definiciones" de bicondicional y disyunción excluyente respectivamente, la segunda es un poco mas fácil de notar.

- Solo por si acaso, para entender mejor la definición de disyunción excluyente recordemos que habíamos quedado en que era la negación de la tabla de verdad de la bicondicional. Su tabla era "VFFV" por lo que negada quedaría "FVVF" que justamente es la tabla del conector lógico mencionado, lo que se ve en la propiedad 6 es solo su forma simbólica.

- 2 y 7 pueden ser comprobados rápidamente al ver la demostración en la imagen.

- Una forma de recordar las equivalencias de 3 y 8 es esta:

Quedamos en que la negación solo afectaba a las proposiciones y los conectores de disyunción débil y conjunción. Ahora quedaremos en que si vemos a una negación que afecta a un paréntesis que tiene 2 proposiciones unidas por una bicondicional o disyunción fuerte, la negación solo afectará a una de las dos proposiciones.

Algo mas visual es así:

Tenemos ~(p ↔ q), recordando lo anteriormente dicho, la negación puede afectar solo a una proposición y pasaría uno de dos casos "~p ↔ q" o "p ↔ ~q".

- Para entender mejor las propiedades 4,5,9 y 10 bastará con ver las demostraciones, podemos comprobar que "p ↔ q" tiene la misma tabla que "~p ↔ ~q" y lo mismo pasa con "p △ q" y "~p △ ~q". Cambiar la posición de alguna de las 2 proposiciones lógicas tampoco afectará en nada a los resultados finales.

Notas finales de la clase de lógica proposicional

Bueno, esa ha sido la primera clase del blog de álgebra, honestamente he demorado muchísimo mas de lo que creía en hacer solo una de las entradas (no conté las horas pero mas de 10 de seguro). De momento el blog es nuevo por lo que no tiene autoridad ante google como para que muchas personas lo vean pero si por alguna razón has llegado hasta aquí, me gustaría saber tu opinión sobre esta "clase", ¿Te ha ayudado? La he hecho a forma de práctica para mí y he tratado de explicarla como si mi alumno fuese alguien que no sabe nada de este tema, acepto sus opiniones y sugerencias que me ayuden a mejorar la calidad de las entradas.

Por otro lado, se que dije que iba a colocar archivos a modo de resumen de cada clase pero creo que tendrá que esperar a un futuro un poco lejano, de momento podrán encontrar la parte 2 de esta entrada con todos los problemas resueltos por mí en el enlace anterior o buscando en la categoría "Problemas" en el archivo del blog.

Si gustan pueden unirse al servidor de discord de los blogs, si encuentran algún error o tienen alguna pregunta, me gustaría que me lo comenten y muchas gracias por leer.